Découvrez nos
ressources

Activité  ludique pour classe avec plusieurs robots : les élèves entraînent les robots à rouler dans un circuit puis une course est organisée. Les élèves apprennent par la manipulation le principe de l'apprentissage supervisé et l'importance de la qualité des données d'entraînement.

[Contenu vidéo à venir]

‍

‍

Introduction

Le Machine Learning est une branche de l’intelligence artificielle qui a pour but de donner la possibilité aux ordinateurs d’apprendre. Un ordinateur n’est pas intelligent, il ne fait qu’exécuter des tâches. On lui décrit sous forme de programmes quoi faire et comment le faire. C’est ce qu’on appelle la programmation.

Le Machine Learning traite des sujets complexes où la programmation traditionnelle trouve ses limites. Construire un programme qui conduit une voiture serait très complexe voire impossible. Cela étant dû aux très nombreux cas possibles à traiter… Le Machine Learning traite cette problématique différemment. Au lieu de décrire quoi faire, le programme apprendra par lui-même comment conduire en “observant” des expérimentations.

Machine Learning : Donner la possibilité à un programme d’apprendre des tâches qui n’ont pas été programmées.

En fonction des données d’expérimentations que prendra l’algorithme d’apprentissage en entrée, il déduira par lui-même une hypothèse de fonctionnement. Il utilisera cette dernière pour de nouveaux cas, et affinera son expérience au fil du temps.

Il existe trois types d‘apprentissages en Machine Learning :

• Apprentissage Supervisé
• Apprentissage Non supervisé
• Apprentissage par Renforcement

L’apprentissage supervisé est le type le plus courant. Il s’agit de fournir aux algorithmes d’apprentissages un jeu de données d’apprentissage (Training Set) sous forme de couples (X, Y) avec X les variables prédictives (ou données d’entrée), et Y le résultat de l’observation (ou décision). En se basant sur le Training Set, l’algorithme va trouver une fonction mathématique qui permet de transformer (au mieux) X vers Y. En d’autres termes l’algorithme va trouver une fonction F tel que Y≈F(X) .

Ainsi, dans une situation X, il saura quelle décision Y doit prendre.

Situation d'étude et training set du robot AlphAI

Il convient désormais de préciser les situations X et les décisions Y attendues. 

Le cas d’étude proposé est le déplacement du robot dans une arène rouge. L’objectif est que le robot se déplace tout seul sans jamais toucher les murs.

Pour cela le robot pourra prendre les décisions suivantes :

• Tourner à gauche 
• Aller tout droit 
• Tourner à droite 

Afin de prendre la décision il faut nécessairement un retour d’information afin de disposer de données (data ou training set).

Cela est donné par les capteurs. Le choix effectué ici est d’utiliser la caméra. De la zone d’image de la caméra il est extrait deux zones qui seront appelées super pixels (voir ci-contre). La quantité de rouge de chaque super-pixel augmente lorsque le robot s’approche des murs en raison du contraste entre la piste blanche et les murs rouges.

‍

‍

Activité 1. Indiquer dans le tableau ci-dessous le résultat attendu comme décision en fonction de ce qui est repéré dans les superpixels.

‍

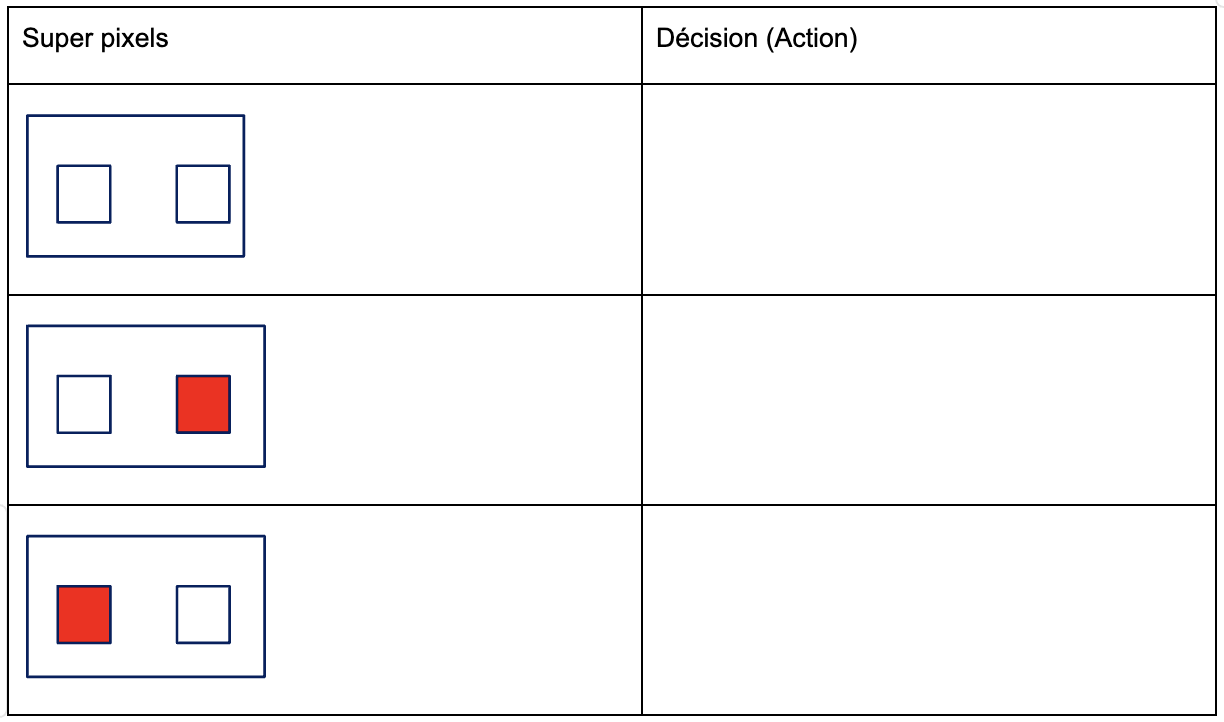
Les cas simplifiés ci-dessus, ne se produisent que très rarement. Pour pouvoir prendre la décision dans tous les cas possibles, il faut obtenir la valeur numérique du niveau de rouge. 

L’image issue de la caméra est de taille 48*64 pixels. La position et la géométrie des super-pixels est définie par la figure suivante :

‍

‍

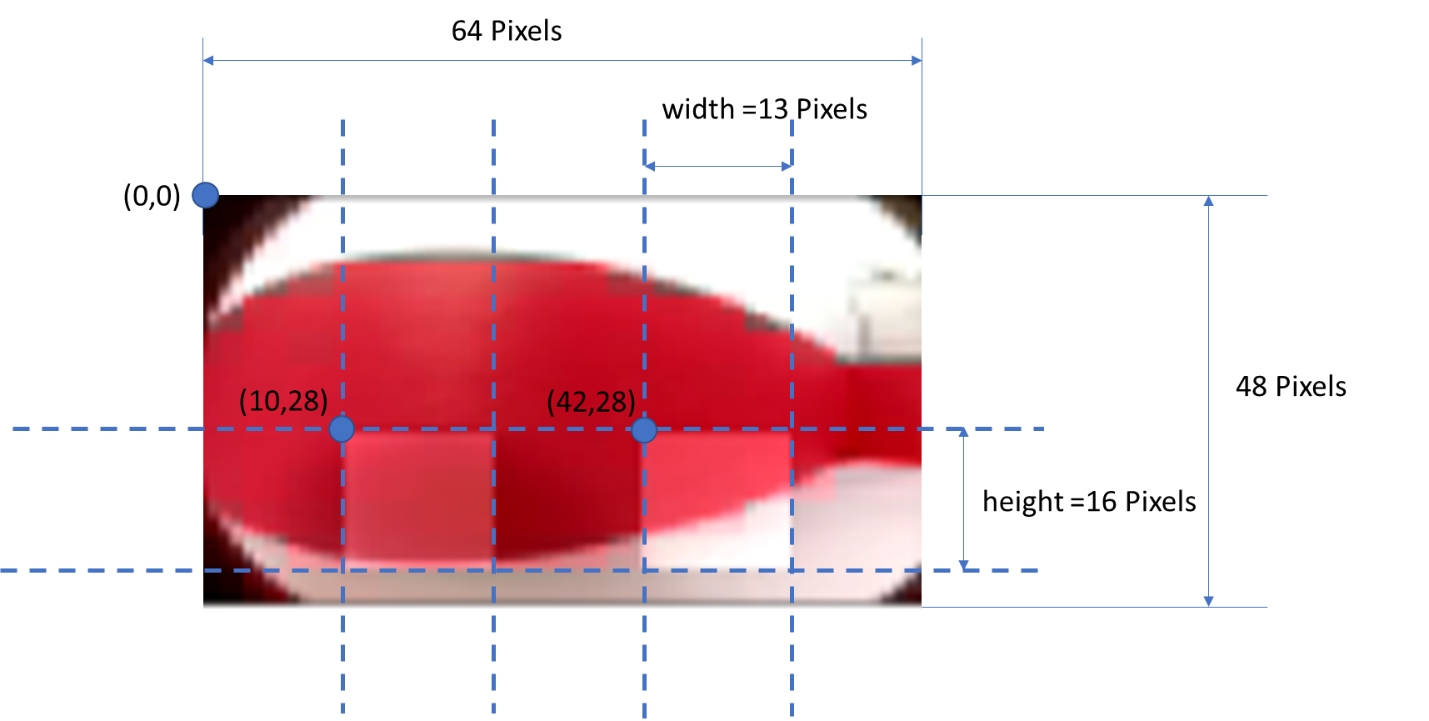
Activité 2. Ouvrir le fichier get_values.py. Indiquer le chemin d’accès de l’image forward_0.jpg et exécuter le code ci-dessous permettant d’afficher l’image dans python.

from PIL import Image

import numpy as np

import matplotlib.pyplot as plt

def read_image(name):

    return np.array(Image.open(name, "r"))

img1=read_image("forward_0.jpg") #indiquer le chemin d'accès de l'image

plt.imshow(img1)

plt.show()

Vous devez obtenir une image de la forme ci-dessous d’une taille de 48 pixels par 64 pixels, codée avec les trois couleurs RVB (Rouge Vert Bleu).

« img1 » est un tableau de pixels de taille 48*64*3

Dans le tableau de pixel on retrouve les 3 niveaux de couleurs Rouge Vert Bleu codés entre 0 et 255.

A partir de cette image, il va falloir extraire les deux super-pixels définis précédemment et déterminer une méthode permettant d’obtenir le niveau de rouge pour chacun.

‍

‍

Nous allons comparer différentes techniques pour obtenir le meilleur contraste entre le rouge et le blanc de chaque super-pixel :

• le niveau de gris moyen de chaque super-pixel
• le niveau de rouge moyen de chaque super-pixel
• le niveau de vert moyen de chaque super-pixel

‍

Dans un premier temps, l’image est transformée en niveau de gris à l’aide de la fonction rgb2gray de la façon suivante :

def rgb2gray(rgb):

    return np.dot(rgb[...,:3], [0.299, 0.587, 0.144])

img2=rgb2gray(img1)

plt.imshow(img2, cmap="gray")

plt.show()

« img2 » correspond à l’image en niveau de gris. Ainsi il n’y a qu’une seule valeur numérique entre 0 et 255 pour chaque pixel. 0 correspond à un pixel blanc et 255 un pixel noir. Les super pixels étant dans la zone « basse » de l’image

‍

‍

Activité 3. Ecrire une fonction moyenne(img,x,y,height,width)   qui va prendre en argument un tableau de pixels « img » à un niveau de couleur, les coordonnées « x » et « y » du pixel en haut à gauche d’un super-pixel, la hauteur « height » et la largeur « width » d’un super-pixel et qui renvoie la moyenne du niveau de couleur du super-pixel. 

‍

Il est ainsi possible de récupérer deux valeurs avec les deux super-pixels définis précédemment à l’aide du code :

def get_two_values(img, x1=10, y1=28, x2=42, y2=28, height=16, width=13):

    value1 = moyenne(img, x1, y1, height, width)

    value2 = moyenne(img, x2, y2, height, width)

    return np.array((value1, value2))

Le niveau de couleur du super-pixel gauche est noté value1, le niveau de couleur du super-pixel droit est noté value2. Il est ainsi possible de définir un point de coordonnées (value1, value2)

‍

‍

Activité 4. Executer le code pour récupérer les valeurs value1 et value2 de l’image en niveau de gris obtenue précédemment.

Le choix effectué dans le logiciel AlphAI est d’utiliser la fonction de python mean qui va calculer la valeur moyenne du tableau.

‍

‍

‍

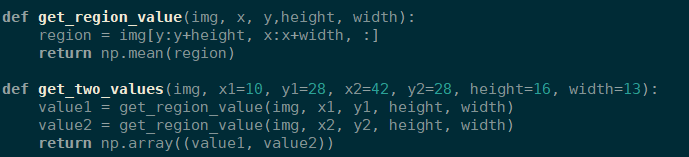
Activité 5. Appliquer la méthode du logiciel AlphAI et celle avec le niveau de gris et compléter avec les valeurs value1 et value2 dans les deux cas.

Fonction mean

Niveau Gris

Forward_0

Forwad_1

Left_0

Left_1

Right_0

Right_1

Right_2

Test_0

Test_1

‍

‍

Activité 6. Placer les points sur le graphique et identifier les zones correspondant aux différentes décisions (tourner à gauche, aller tout droit, tourner à droite). Conclure sur la méthode qui vous semble la plus appropriée pour distinguer les différentes décisions.

Intensité super-pixel droit

Intensité  super-pixel gauche

‍

À ce stade, il serait possible de piloter le robot à partir d’actions conditionnelles portant sur ces valeurs de super-pixels. L’approche va être différente dans la suite. Nous allons utiliser une méthode portant le nom d’algorithme des K plus proches voisins.

‍

‍

L’algorithme des k plus proches voisins, KNN

Nous allons étudier de près un algorithme très connu parmi les algorithmes de machine learning : l’algorithme des K plus proches voisins, ou KNN en anglais pour « K Nearest Neighbours ». Cet algorithme a l’avantage d’être très simple, et donc de fournir une bonne base pour comprendre l’apprentissage supervisé.

L'idée est d'utiliser un grand nombre de données afin "d'apprendre à la machine" à résoudre un certain type de problèmes. L’algorithme est particulièrement intuitif quand les données se présentent comme des points dans un espace de dimension 2, qui pourront donc être affichés à l’écran. Nous allons donc choisir une configuration avec seulement 2 entrées capteurs, à savoir 2 « super-pixels » de la caméra afin de permettre au robot de repérer les murs et de circuler dans l’arène sans blocage. Dans un premier temps ce sera à nous d’indiquer au robot l’action associée pour chaque nouvelle donnée (2 « super-pixels »), mais ensuite il sera capable de circuler par lui-même en choisissant l’action majoritaire prise par les K plus proches voisins parmi les données entrées pendant la phase d’entraînement.

Cet algorithme d’apprentissage supervisé permet de classifier des données en fonction de leur proximité avec celles existantes constituant les données d’entraînement. Les nouvelles données considèrent k voisins, les k plus proches, pour choisir quelle classification appliquer. Avec des données discrètes, comme des points dans un plan ou dans l’espace, les plus proches voisins sont sélectionnés en utilisant la distance euclidienne, mais d’autres méthodes peuvent être utilisées dans d’autres situations, comme la distance Manhattan si les données se placent sur un quadrillage ou un échiquier. L’intérêt de cet algorithme réside dans le choix de k : trop petit et l’algorithme devient trop sensible aux erreurs ou aux données manquantes, trop grand et il considère des données qui ne devraient pas être considérées.

On peut schématiser le fonctionnement de k-NN en l’écrivant en pseudo-code suivant :

Début Algorithme

Données en entrée :

• un jeu de données D, correspondant au training set élaboré
• une fonction de calcul de distance entre les deux points considérés de coordonnées [x1,y1] et [x2,y2]. d=x2-x12+y2-y12
• Un nombre entier k, représentant le nombre de voisins à prendre en compte

Pour une nouvelle observation X dont on veut prédire sa décision Y Faire :

1. Calculer toutes les distances de cette observation X avec les autres observations du jeu de données D
2. Retenir les K observations du jeu de données D les plus proches de X en utilisation la fonction de calcul de distance d
3. Prendre les valeurs de Y des k observations retenues. Effectuer une régression et calculer la moyenne (ou la médiane) de Y retenues 
4. Retourner la valeur calculée dans l’étape 3 comme étant la valeur qui a été prédite par K-NN pour l’observation X.

Fin Algorithme

Il faut donc pouvoir calculer la distance entre deux points. Dans un graphique en deux dimensions comme c’est le cas dans notre exemple, cela correspond simplement à la norme du vecteur entre les deux points.

Activité 1. Ecrire la fonction distance(point1, point2)   qui prend en argument deux points (point1=[x1,y1], point2=[x2,y2])  et qui renvoie la distance entre ces deux points.

Activité 2. Compléter le tableau ci-après en déterminant la distance entre les super-pixels des images précédentes (forward_0.jpg, forward_1.jpg,…) et des deux images tests (test_0.jpg et test_1.jpg).

‍

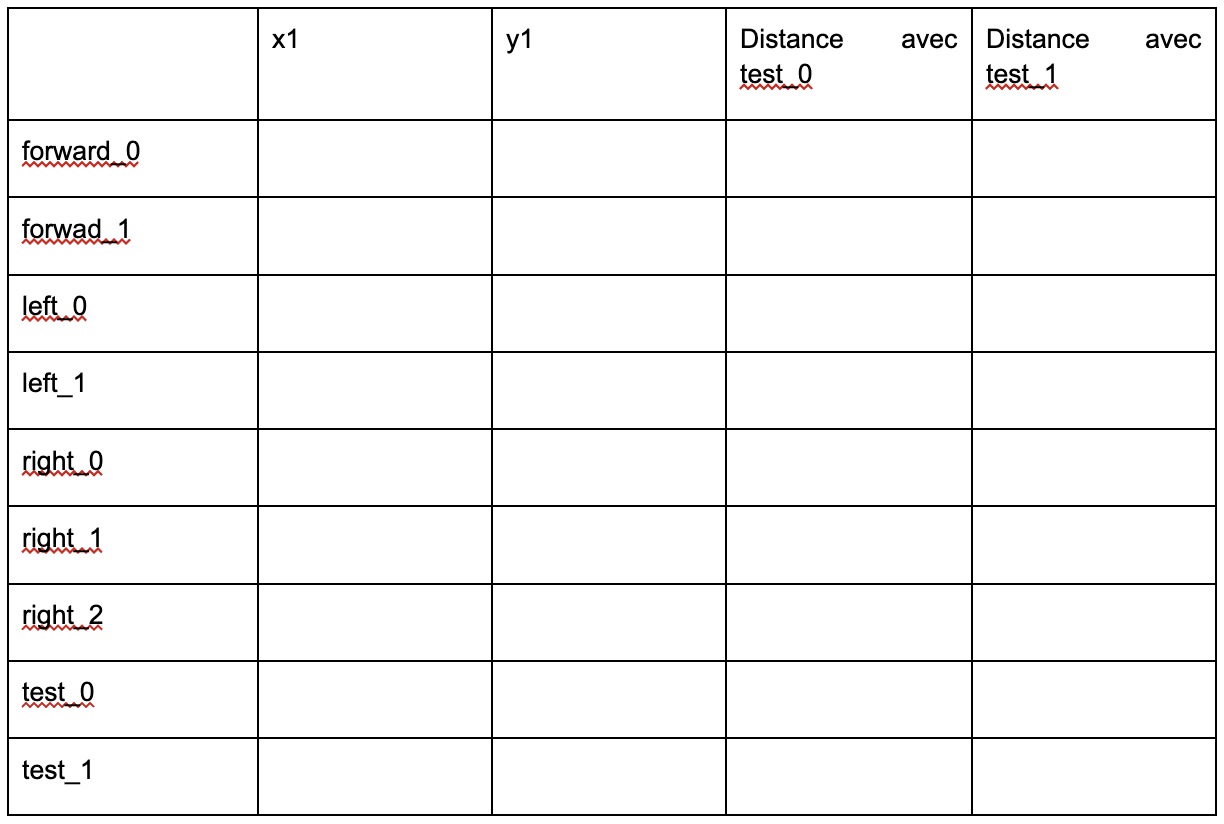
Activité 3. Appliquer les étapes 3 et 4 de l’algorithme K-NN en en prenant K=1,2,3 et 4 et en déduire la décision qui doit être prise (aller tout droit, tourner à gauche, tourner à droite).

‍

‍

Entrainement du robot

Phase de préparation de l’environnement de travail

• Dans le menu Paramètres - > Charger des configurations d'exemples, sélectionner la configuration exemple « apprentissage supervisé - KNN Caméra». 

Attention : Pour ce scénario, afin d’obtenir le meilleur contraste possible, mettez une surface blanche au sol, et Assurez-vous d’avoir un éclairage uniforme sur la surface de l’arène.

‍

Phase d’entraînement

Activité 1. Suivre le protocole afin de réaliser la phase d'entraînement

‍

Vous êtes maintenant connecté au robot, et votre écran doit ressembler à l’image ci-dessous. Le niveau de sa batterie doit s’afficher en bas à droite (vérifiez que le robot est bien chargé).

• Tant que le robot a de la place pour avancer, appuyez sur aller tout droit. 

• Si le robot s’approche d’un mur, appuyez sur virage sur place à gauche ou à droite. 

À chaque instruction envoyée au robot, un nouveau point est ajouté au graphique. L’abscisse de ce point correspond à la valeur du super-pixel de gauche et son ordonnée correspond à la valeur du super-pixel de droite. La couleur de chaque point correspond à l’action choisie : jaune pour aller tout droit, vert pour tourner à droite et rouge pour tourner à gauche. Ces points sont les données d’entraînement. Cette phase d’entraînement est primordiale pour que l’IA puisse apprendre correctement. Si les données d’entraînement contiennent trop d’erreurs ou d’approximations, le comportement de l’IA risque de ne pas être satisfaisant. 

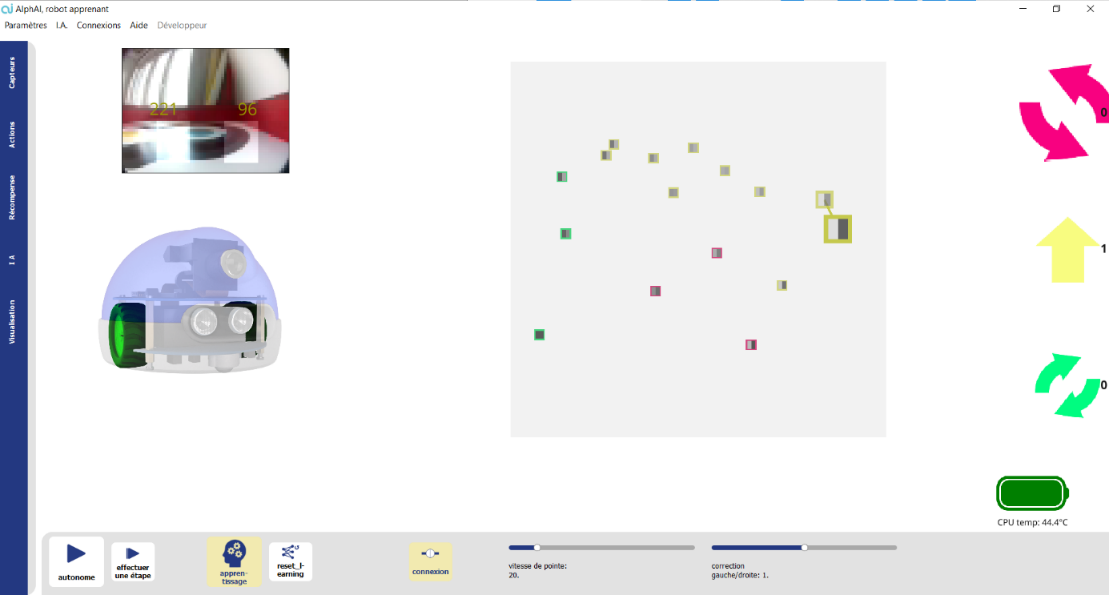
Notez bien :

Les pixels deviennent plus sombres lorsque le robot s’approche des murs. Normalement si le pixel de gauche est le plus sombre, il faut tourner à droite, et si le pixel de droite est le plus sombre, il faut tourner à gauche. Après avoir ajouté quelques points sur le graphique, vous pouvez activer la couleur d’arrière-plan dans l’onglet des paramètres de visualisation. Cette option colore chaque pixel du graphique de la couleur du point de donnée le plus proche.

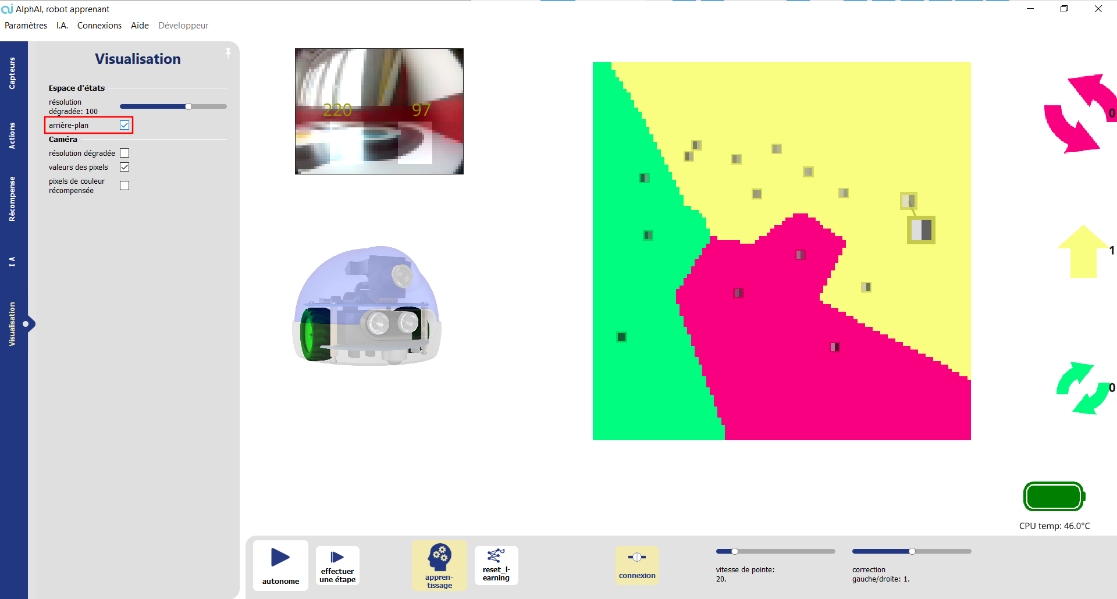
Lorsque vous aurez trois régions bien claires sur le graphique, arrêtez la phase d’entraînement et réactivez l’autonomie pour passer à la phase de test.  Ne pas hésiter à bouger le robot à la main, lorsqu’une zone du graphique contient trop peu de points.

‍

‍

Tests

Si le robot est bien entraîné, il saura éviter les bords par lui-même. Si au contraire il est mal entraîné ou la luminosité dans l’arène n’est pas homogène, cela va produire du bruit dans les régions créées et le robot fera plus d’actions inappropriées.

Notez bien :

Afin d’obtenir le meilleur comportement du robot, il faut tester plusieurs valeurs de k. Pour changer cette valeur, allez dans l’onglet « IA » et changer la valeur du paramètre « nombre de voisins ».

Une bonne valeur de k réduit l’effet du bruit et permet au robot de mieux gérer les régions inexplorées.

Une fois que le robot est bien entraîné et que les tests se déroulent bien, vous pouvez passer aux activités.

‍

Activité 1. Comparez le comportement du robot avec k=1, k=3, k=10 et k=30. Ensuite, d’après ce que vous constatez, essayer de déterminer la valeur de k qui minimise l’effet des erreurs et donne le meilleur comportement du robot, c’est-à-dire la plus grande distance parcourue sans heurter un mur. La bonne valeur va dépendre du nombre de points de données, et du nombre d’erreurs dans ces données.

‍

Activité 2. Maintenant que vous avez bien compris l’algorithme, essayez d’entrainer le robot avec le minimum de données possibles qui lui permettent de tourner sans taper contre les murs. 

‍

Commencez par faire une version théorique en dessinant les zones que vous voudriez obtenir sur votre graphique. Quels points sont à placer pour la réaliser ? Testez ces points avec le robot après les avoir rentrés dans le logiciel. Votre modèle théorique a-t-il été applicable à la réalité, ou avez-vous dû y faire des modifications ? Quelles sont les limitations de cette méthode pour un robot tel que celui-là ?

Astuce : Vous pouvez déplacer le robot à la main pour choisir les points que vous voulez lui apprendre.

Remarque : Nous avons réussi à apprendre au robot à circuler dans l’arène sans taper les murs avec 3 points seulement.

Pour aller plus loin :

‍

Activité 3. S’il vous reste du temps et que vous voulez expérimenter, changez d’algorithme et regardez quelles différences le robot a dans son comportement par rapport à KNN. Quel autre algorithme proposé à un apprentissage plus rapide ? Et quel autre algorithme permettrait, selon vous, l’apprentissage de tâches plus complexes, comme taper dans un ballon vert ou reconnaître des ordres communiqués avec des signes de la main ?

‍

‍

Programmer l’algorithme des K plus proches voisins

1. Stoppez le robot et réactivez le bouton « Autonome ».

2. Dans l’onglet IA, sélectionnez  Algorithme : code élève , cela ouvrira une nouvelle fenêtre vous demandant de nommer le fichier. 

3. Après lui avoir donné un nom, le fichier apparaît dans l’explorateur Windows : ouvrez-le dans votre éditeur de code préféré (Spyder, par exemple).

Ce code présente 3 fonctions déjà existantes : init, learn et take_decision. Ces fonctions seront appelées par le logiciel principal. Seule la fonction take_decision est importante pour ce TP.

4. Remarquez que quand vous vous déconnectez, un mini-robot simulé apparaît en bas à droite. Si vous le voulez, vous pouvez faire les questions ci-dessous avec ce mini-robot et revenir au vrai robot à la fin du TP ; mais vous pouvez aussi faire tout le TP en restant connecté au vrai robot : comme vous préférez !

‍

‍

PROGRAMMER LE ROBOT DIRECTEMENT

Avant de programmer une intelligence artificielle, commençons par comprendre le principe de la fonction take_decision. Vous allez pouvoir modifier cette fonction pour changer le comportement du robot : après chaque modification, sauvegardez votre code et cliquez sur le bouton « Réinitialiser l’IA ». Cette étape est à répéter pour chaque modification du code : sauver puis recharger le code.

La fonction a le prototype suivant :

take_decisionsensors:listint

L’entrée sensors est l’état des capteurs du robot, c’est-à-dire dans notre cas une liste de deux valeurs sensors[0] et sensors[1] qui sont l’intensité de ce que voit le robot à sa gauche et à sa droite. Sa sortie est le numéro de l’action choisie.

1. Ajoutez l’instruction print(sensors) à l’intérieur de la fonction. Sauvegardez, cliquez « Réinitialiser l’IA » dans le logiciel, et démarrez le robot. La valeur de sensors s’affiche maintenant dans la console (cliquer dans la barre des tâches sur l’icône pour afficher la console). Quelle est à peu près la valeur de sensors quand le robot est face à un mur ? quand il n’est pas face à un mur ? quand il y a un mur à sa gauche ou à sa droite ?

‍

2. Pour l’instant la fonction renvoie 0. Quelle valeur faut-il renvoyer pour que le robot aille tout droit ? (Faites l’essai)

‍

3. Utilisez la variable x pour programmer un comportement cohérent du robot : « s’il n’y a pas de mur, je vais tout droit ; s’il y a un mur, je me tourne. »

‍

‍

PROGRAMMATION DE L’ALGORITHME

Calcul de distance

Si vous ne l’avez pas déjà fait lors de l’activité précédente, programmez une nouvelle fonction distance qui prend comme arguments deux points a et b qui sont deux tableaux de deux éléments chacun contenant leurs coordonnées et qui renvoie la distance euclidienne de ces deux points. Le prototype de la fonction est le suivant :

distancea:list, b:listfloat

Avec a=x1, y1 et b=x2, y2

Pour rappel, la distance euclidienne entre ces deux points est : d=x2-x12+y2-y12.

La racine carrée peut être utilisée en Python en important la bibliothèque math (ou numpy) en haut du fichier :

import math

et s’écrit ainsi :

y = math.sqrt(x)

L’opérateur carré peut être fait de la façon suivante :

y = x**2

4. Programmez la nouvelle fonction distance. Puis pour la tester, écrivez en bas du fichier :

# compute distance

a = [0, 0]
b = [1, 2]
print("distance", distance(a, b))

Sauvez, chargez le code avec « Réinitialiser l’IA » et notez ci-dessous le résultat qui s’affiche dans la console :

‍

Calcul de toutes les distances

Maintenant que vous avez une méthode pour calculer une distance, écrivez une nouvelle fonction all_distances qui calcule toutes les distances d’un point par rapport à la variable train_sensors qui sont les données d’entrée d’entrainement. Cette fonction prendra comme argument un nouveau point x qui est une liste de deux éléments comme précédemment, et renverra un tableau contenant toutes ces distances. Son prototype est :

all_distances(a:list[float], train_sensors:list[list[float]])→list[float]

Avec a=x0, y0 et train_sensors=x1, y1, x2, y2, …, xn, yn Le tableau train_sensors étant de longueur n.

‍

5. Programmez all_distances, puis testez avec le code suivant en bas du fichier :

# compute all distances

a = [0.4, 0.6]

train_sensors = [[0, 0], [0, 1], [1, 0]]

distance_list = all_distances(a, train_sensors)

print('distances to data', distance_list)

Rechargez le code et recopiez votre résultat :

‍

Trouver le plus petit element d’un tableau

Créez une fonction s’appelant find_minimum prenant comme unique argument un tableau et renvoyant l’indice du premier plus petit élément. Son prototype est :

find_minimum(dlist:listfloat)→int

6. Programmez et testez find_minimum avec le code suivant :

# minimum in a list

idx_min = find_minimum(distance_list)

print('index of minimum', idx_min)

Notez le résultat :

‍

Le plus proche voisin

Maintenant que nous avons toutes les fonctions nécessaires, nous allons pouvoir créer la fonction nearest_neighbor_decision qui prend comme argument les données d’entrainement et l’entrée de la caméra actuelle, et qui renvoie la commande à envoyer au robot. Son prototype est :

nearest_neighbor_decision(train_sensors:list[listfloat],train_decisions:list[int],a:list[float])→int

Comme précédemment, a=x0, y0 et  train_sensors=x1, y1, x2, y2, …, xn, yn et train_decisions = d1,…,dn où chaque di est la décision prise pour le point xi, yi dans le tableau train_sensors. 

Pour réaliser la fonction, calculez les distances, trouvez la plus courte et renvoyez la commande associée en utilisant train_decisions.

‍

7. Programmez et testez nearest_neighbors_decision avec le code suivant :

# KNN

a = [0.4, 0.6]

train_sensors = [[0, 0], [0, 1], [1, 0]]

train_decisions = [1, 2, 0]

decision = nearest_neighbor_decision(train_sensors, train_decisions, a)

print('KNN', decision)

Recopiez le résultat :

‍

‍

UTILISATION DE VOTRE ALGORITHME AVEC LE ROBOT 

Félicitations, vous avez programmé vous-mêmes l’algorithme des K plus proches voisins dans le cas K=1. Il ne vous reste plus qu’à l’utiliser dans le programme pour entraîner le robot.

Pour cela, recopiez les lignes ci-dessous pour programmer la fonction take_decision pour prendre les bonnes décisions, mais également learn pour se rappeler des données d’entraînement train_sensors et train_decisions qui seront créées au fur et à mesure dans le programme principal :

train_sensors = train_decisions = None

def learn(X_train, y_train):
    global train_sensors, train_decisions
    train_sensors, train_decisions = X_train, y_train
    loss = 0
    return loss

def take_decision(sensors):
    if train_sensors is None:
        return 0
    return nearest_neigbor_decision(train_sensors, train_decisions, sensors)

 Et à présent, vous pouvez entraîner votre robot !

1. Rechargez votre code

1. Désactivez l’autonomie du robot en cliquant sur l’icône

1. ,
2. Dirigez le robot en cliquant sur les flèches à droite de l’écran. Tournez quand le robot est proche des murs et allez tout droit sinon. 

Les tableaux train_sensors et train_decisions sont remplis automatiquement par le logiciel à chaque fois que vous cliquez une flèche.

4. Après un court apprentissage, réactivez l’autonomie

4. Le robot navigue seul dans l’arène. Évite-t-il les murs par lui-même ?

‍

‍

Pour aller plus loin

L’algorithme que vous avez écrit utilise le plus proche voisin pour prendre sa décision. Modifiez votre code pour qu’il prenne en compte la majorité des décisions prises entre un nombre k>1, k∈N. La difficulté réside dans la modification de la fonction trouvant le minimum. Il faut maintenant qu’elle en trouve k et non juste 1.

‍

‍

Bilan et retours d'expérience

‍

En programmation, la liste des fonctions accessibles d’un programme s’appelle API, pour Application Programming Interface, Interface de Programmation d’Application. Elle est utilisée par les programmeurs pour savoir comment interagir avec le programme. Vous trouverez l’API du module python alphai en suivant ce lien : https://drive.google.com/file/d/1C4ovPW_eH5KFz5Y9JvSrzLhtmdOpcp6-/view